вычислением ronz для кулоновского поля некомпенсированного заряда EQ = —2^, дает

^ r

заниженный результат величин Zie и плотности среды, требуемых для выполнения условия (23), поскольку поле EQ много больше реального самосогласованного поля (рис.4).

1.0

Ez/Esph

0.6

0.0 -0.2 -0.4 -0.6 -0.8 -1.0

-8-6-4-202468

z/r0

Рис.4 Распределение электрического поля по радиусу в различные моменты времени для случая 1 на рис.1,2 (жидкая фаза, N = 6.58х1022 см-3 при Т =20 К ), Esph = 207 кВ/см, r0 = 6.67х10-6см;

1 - t = 104нс, 2 - t = 103нс, 3 - t = 102нс; 4 -поле некомпенсированного заряда Zei = 1000 .

0.4 -г 0.3 -0.2 0.1

0.0 --0.1 --0.2

-0.3 Н -0.4

-10 -8 -6 -4 -2 0 2 4 6 8 10 z/r0

Рис.5 Распределение электрического поля по радиусу в различные моменты времени для случая 3 на рис.1,2 (газообразная фаза, N = 1021 см-3 при Т = 300 К ), Esph = 388 В/см, r0 = 4.39х10-4см;

1 - t = 0.1 нс, 2 - t = 1 нс, 3 - t = 10 нс, 4 - t =

100 нс.

На рис.4 для различных моментов времени представлены распределения самосогласованного электрического поля вдоль оси симметрии облака для случая 1, когда все электроны в итоге возвращаются в область ионизации, а на рис.5 - для случая 3, когда временная фаза возврата электронов снова сменяется фазой разлета. Для сравнения, на рис.4 показано также поле некомпенсированного заряда Eq (кривая 4). Значения поля нормированы на величину Esph, -

то есть на величину поля, получающуюся на границе равномерно заряженной с плотностью n0 сферы радиуса rD:

Esph = 3nen0rD

(24)

на

краю

r0L

sph

r

Максимальное значение поля наблюдается в зоне разделения зарядов, некомпенсированного ионного остатка, и оказывается порядка Esph, если rD/r0< 1, и E

если rD/r0>1.

В случае 1 (рис.4) сначала, на стадии разлета электронов, поле возрастает и достигает максимума к моменту времени 10 нс, когда их разлет сменяется возвратом. После этого поле уменьшается из-за компенсации заряда ионов зарядом вернувшихся электронов. Кроме того, максимум поля смещается в сторону периферии области, где остается дебаевское разделение зарядов.

В случае 3 (рис.5) начальная стадия изменения поля такая же, как в предыдущем случае. Начинающийся с момента времени t « 1 нс возврат электронов слегка уменьшает величину

электрического поля (кривые 2 и 3 на рис.5). Поскольку в случае 3 ronz/rt « 1 (см. рис.3), то даже небольшого уменьшения поля достаточно, чтобы электроны снова стали разлетаться из-за ослабшего притяжения к ионному остатку. Установившееся в итоге поле (кривая 4) мало отличается от максимального (кривая 2) и является полем ионного остатка, частично компенсированным вернувшимися электронами.

4.2 Разлет электрон-ионного облака в Ne и Ar

В этом пункте представлены результаты расчета динамики разлета электрон-ионного облака в Ne и Ar с использованием реальных зависимостей от энергии коэффициентов подвижности и диффузии электронов. Выбор этих сред для анализа продиктован тем, что в неоне подвижность электронов положительная во всем диапазоне энергий электрона, а в аргоне может наблюдаться эффект отрицательной подвижности из-за хорошо выраженного минимума Рамзауэра в зависимости транспортного сечения рассеяния электронов на атомах Qm от энергии (рис.6).

В используемом уравнении переноса электронов коэффициенты подвижности и диффузии определяются выражениями [12]

Т^ 2e } -Jms df0 ,^2 } -Jms , ,

3m -W2NQm(s) ds3m 0 V2NQm(s)

где f0(s) - сферически симметричная часть функции распределения электронов по энергиям,

со

с условием нормировки jyfsf0(s)ds = 1.

0

В решаемой задаче об эволюции электронного облака число электронов невелико, их взаимодействием можно пренебречь, таким образом, фактически решается задача о перераспределении в пространстве отдельно взятых электронов, то есть в каждой точке пространства есть только один электрон с энергией s(^). Этому случаю естественным образом соответствует функция распределения электронов по энергиям

f0(s) = -±7 *(*-s(0).(26)

Для такой функции распределения, в соответствии с определением (25), коэффициенты подвижности и диффузии равны

В случае достаточно больших положительных значений iQm /is , подвижность электронов

становится отрицательной, что и наблюдается в Ar в диапазоне энергий электрона от 0.35 до 3 эВ (рис.6). В этом случае электроны дрейфуют не против, а по направлению поля.

Данные для транспортных сечений рассеяния электронов в Ar и Ne взяты из работы [13]. Эти данные представлены на рис.6 сплошными линиями. Рассчитанные по ним с помощью соотношения (27) зависимости подвижности электронов от энергии при нормальной

19 3

плотности N = N0 = 2.69x10 см показаны на рис.6 пунктиром.

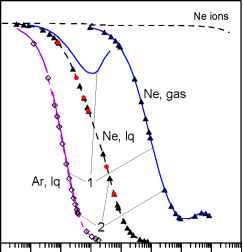
Результаты расчета нормированной плотности электронов в центре области для реальных зависимостей коэффициентов подвижности и диффузии электронов от энергии в Ne и Ar представлены на рис.7 для жидкой и газообразной фазы неона и жидкой фазы аргона.

Основной объем расчетов выполнен для случая отсутствия внешнего электрического поля, Eout = 0, в двух вариантах: без учета (сплошные кривые 1) и с учетом электрон-ионной рекомбинации (пунктирные кривые с треугольными или ромбическими символами 2).

Е

о

из 0 о

Ё

О

4

3 2

1 » >

0 Е

О

-1°

ф

-2*

-3 -4

-5

—1 I Г~П I I I I I I I I I I I I

0.11.010.0

energy, eV

Рис.6 Зависимость транспортного сечения рассеяния электронов [13] (сплошные линии) и подвижности электронов при нормальной плотности N = N0 = 2.69х1019 см3 (пунктир) от энергии электронов в Ar и Ne.

о С

о" II

о" II

,><,

"с"

1.1

1.0 0.9 0.8 Н 0.7 0.6 0.5 0.4 0.3 Н 0.2

0.1 0.0

I мши I шип

1E-5 1E-4 1E-3 1E-2 0.1

time, ns

1 1E+1 1E+2 1E+3

Рис.7 Зависимость от времени нормированной плотности электронов в центре области в Ne и Ar; сплошные кривые 1 - без учета рекомбинации, Eout = 0, символы 2 - с учетом рекомбинации, Eout = 0, кружки - с учетом рекомбинации, Eout = 80кВ/см ; Ar, lq - для жидкой фазы аргона (N = 2.1 х1022 см3 при Т = 87 К), Ne, lq - для жидкой фазы неона (N = 6.58х1022 см-3 при Т =20 К), Ne, gas - для газообразной фазы неона (N = 1021 см-3 при Т = 300 К)._

При описании рекомбинации учитывались как тройная рекомбинация с участием атома или электрона в качестве третьей частицы, с коэффициентами рекомбинации ara [14] и are [15], соответственно, так и диссоциативная рекомбинация, поскольку мюонный ион при

213

рассматриваемых плотностях среды выше N = 10 см кластерным ионом.

Коэффициенты тройной рекомбинации рассчитывались по формулам [14,15]

является молекулярным или

ra

32>/2Л e6N TjmQm (Te)

3

M

8^V2n e10 ne Л

9yfm t/

(28)

где Л « 0.3 - кулоновский логарифм для связанных состояний. Приведенное численное значение для Л подобрано так, чтобы обеспечить совпадение теоретического are с экспериментальными данными [15]. Выражения (28) дают следующие расчетные формулы для вычисления ara и are:

а

ra

1.83-10-

N (cm3) T (eV)Qm (1016cm2) cm3

Te7/2(eV)

M (a.e.)

(29)