Определяющие соотношения для реономных материалов с "перманентной памятью"

Кузнецов В.Н., Агахи К.А. fkamilla@imec.msu.ru), Басалов Ю.Г., Ковальков В.К., Шестериков С.А.

Институт механики МГУ им. М.В. Ломоносова

Работа выполнена при поддержке гранта № 04-01-00325 Российского Фонда Фундаментальных Исследований.

Предлагаются определяющие соотношения для описания реологических процессов деформирования, зависящих от времени (ползучесть, релаксация, нелинейно-вязко-пластические эффекты). Эти соотношения являются дальнейшим развитием определяющих соотношений, построеных авторами в работах [1-2] и основанных на результатах американских исследователей Фицджеральда (70-е годы), который следовал идее Коулмена и Нолла (60-е годы). Частично близкую идею высказал в 1943 году советский ученый Н.М. Беляев.

Вводится обобщенная деформация в безразмерных координатах у = \s\a V\sf , где s

деформация, а, p, £ - константы, jsfp - обобщенная норма Лебега:

1

Здесь y(t) — весовая функция, а <p(t) — нормирующая функция. Материальные функции <p(t) и y(t) определяются экспериментально. Таким образом, у есть нелинейный оператор по времени t, зависящий от <р, у/, p . Напряжение а и деформация s связаны следующим соотношением:

a(t) = F (у) + A 1 -t^lj K (t -r)s(r)dr(1.1)

V Smax J 0

Здесь smax - максимальное значение s(t) на отрезке [0, t], A1 - константа, K - ядро

оператора Вольтерры, F - материальная функция. Второе слагаемое в (1.1) описывает разгрузку или, точнее, процессы с убывающей деформацией. Когда деформации не убывают, второе слагаемое (1.1) обращается в ноль, так как s(t) = smax и определяющие соотношения (1.1) принимают следующий вид:

a(t) = F (у)(1.2)

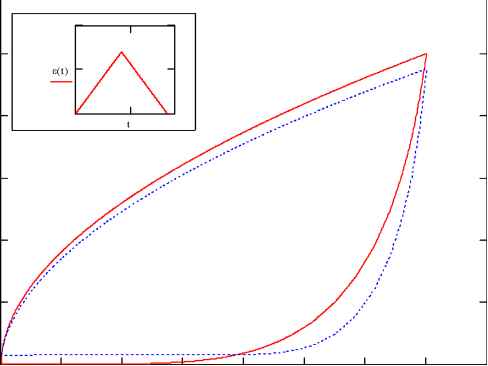
В опыте с постоянной скоростью деформирования это соотношение должно описывать кривую напряжение-деформация, что позволяет определить функцию F . На графиках 1-2 представлены сравнения результатов экспериментов Фицджеральда и расчетов по соотношению (1.1) (сплошная линия - эксперимент, пунктирная - расчёт).

0

аF ( s , t) а(s,t)

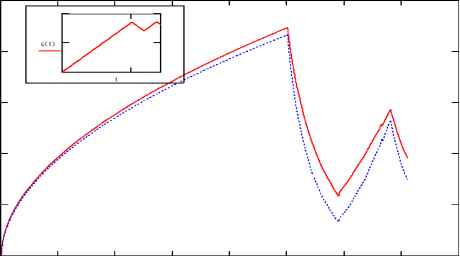
Рисунок 1. Зависимость напряжений от времени в опыте со сложной программой по

деформации (s = 0.0342 ) 12i-1-1-1-1-1-1-1-1

10

aF( s, t) а(s,t)

0.001

0.002

0.003

0.004

s(t)

0.005

0.006

0.007

0.008

Рисунок 2. Кривая деформирования в опыте со сложной программой по деформации

(s = 0.0169, t1 = 0,4146min)

Пластические эффекты, прежде всего, наличие критического значения деформации, после которой возникает пластическое течение (наряду с вязким течением) учитывается следующим образом. Условие пластичности принимается как обобщение условия Мизеса, учитывающее влияние скорости деформирования, в следующем виде: s = es (1 + h(s)) (в

трехмерном случае eu = es (1 + heu), eu = ^eiJeiJ). Здесь h - экспериментальная функция, etj - девиатор тензора деформаций.

25

20

15

10

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

8

6

4

2

0

0

При условии s< es принимаем, что разгрузка описывается уравнением (1.2) и является нелинейной, но пластические деформации при этом отсутствуют; если s > es, разгрузка описывается соотношением (1.1) и при этом имеют место пластические деформации. В простейшем случае у/ = 1, <p(t) = , № > 0 • Тогда для деформирования с постоянной

скоростью s = at, a = const мы имеем а = E(a) ■ s в случае s < es и а = E(a) ■ (1 - с (s)) • s в случае s > es. Здесь E обозначает модуль упругости, зависящий от скорости деформирования a, с - функция пластичности Ильюшина [4] (c(s) = 0 в случае s < es, c(s) > 0 в противном случае).

В общем случае нагружения, когда s Ф const, определяющие соотношения при нагрузке записывается подобно тому, как это делается в теории пластичности малых упруго-пластических деформаций Генки- Ильюшина:

0, s< es

При s > es а = F- с(у)), с(у)

F (г±-Ф(г)

F(y)

s > e„

F и Ф находятся из опыта на растяжение с постоянной скоростью, когда у = at, причём F(у) при s < es есть экспериментальная кривая, для которой выбирается аналитическая аппроксимация, допускающая аналитическое продолжение при s > es (в теории Ильюшина F - линейная функция).

F(у) , Ф(у) для опыта на сдвиг с постоянной скоростью показаны на рисунке 3

экстраполяция начального участка

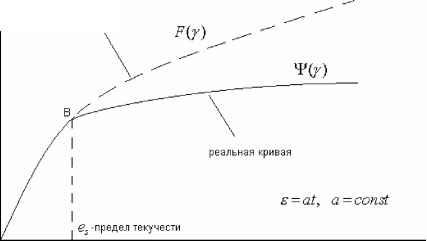
0А

диапазон

нелин.

вязко-упруго сти

диапазон вязкоупругость+пластичность

Таким образом, определяющие соотношения имеют вид:

а = ¥(у) + (1 - s/smaX) \ K (t - r)s(r)dr Ч (У) = F (у)(1 -с(у))

(1.3)