дополнительно к приведенным штрафам была предложена мера структурной схожести («по Журавлеву») участков траекторий, принимающая значение 1 или 0.

Сам алгоритм динамического программирования состоит из двух последовательных действий: прямого прохода, когда ищется локально-оптимальное

Рис.5. Пример сопоставления двух траекторий.

продолжение траектории и обратного прохода, когда выбирается путь, доставляющий минимальный суммарный штраф за несоответствие двух траекторий.

Поскольку в прямом проходе алгоритма имеет смысл находить соответствие только между вертикальными экстремумами одинакового типа, то из ячейки (ij) возможно продолжение в одну из трех ячеек:(i+1j+3), (i+3j+1). На рис. 5 представлен

тестовый пример составления таблицы штрафов при поиске оптимального соответствия (в реальной ситуации, естественно, размер таблицы является большим). В каждой ячейке таблицы (i,j) может находится до трех «подтаблиц», содержащих штрафы за сопоставления хорд с учетом возможной вариативной трансформации 1-го рода. Таким образом, предложенный способ прямого прохода алгоритма является по своей сути иерархическим: в таблицу штрафов заносятся меры отличия участков с учетом пропуска двух экстремумов. При этом при нахождении штрафов такого рода также ищется оптимальное соответствие между экстремальными точками с той лишь разницей, что это не обязаны быть вертикальные экстремумы. Именно в силу последнего обстоятельства алгоритм поиска экстремальных точек был разработан с особой тщательностью [1].

На рис.5 представлен оптимальный путь (0,0) (1,3) (2,4) (4,5), реализующий пропуск экстремальной точки под номером 4 для верхней кривой.

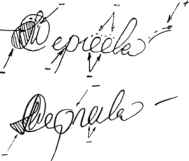
Рис.6. Пример разборки подписи экспертом-криминалистом.

Анализ формы траектории

В результате работы алгоритма сопоставления появляется набор гипотез для отбора кандидата на роль эталонной подписи. В силу того, что мера, по которой находятся структурные несоответствия достаточно «нестрогая» (исключающая лишь грубые несоответствия), то для тщательного анализа желательно проводить более детальное исследование кривых. В этой связи интересно обратиться к опыту экспертов-почерковедов.

При криминалистической экспертизе подписи [6], после того как были установлены общие признаки, «.. .эксперт проводит анализ частных признаков таких как:

•размеры углов (острые, тупые, прямые)

•степень кривизны дугообразных элементов (определяется измерением угла, образованного касательными от оснований дуги до их пересечения, а по углу определяется степень кривизны данной дуги)

•размещение росчерка и его элементов относительно подписи в целом (выше подписи, ниже, на уровне ее)».

На рис.6 приводится образец разборки подписи проведенной экспертом. Из данного рисунка, а также из приведенной цитаты следует, что для оценки формы кривой необходимо уметь описывать ее локальные особенности. Одним из лучших вариантов здесь является использование кривой Безье, получившей широкое распространение в компьютерной графике. Причем заметим, что приведенная выше цитата фактически описывает сплайн Безье, т. к. касательные к концам сплайна совпадают с отрезками, соединяющими соответствующие контрольные точки и концы сплайна.

Было установлено, что хотя для многих случаев поведения траектории «полный» метод наименьших квадратов (основанный на нахождении обратной матрицы размером 4x4 методом LUP-разложения), и «упрощенный» метод наименьших квадратов (использующий сведения о концах траектории и позволяющий в явном виде записать обращение матрицы размером 2х2) дают удовлетворительные результаты, они требуют уточнения. В результатебылреализован

итерационный метод нахождения кривой Безье для аппроксимации участка траектории. На рис.7 представлен случай петлевого элемента, для которого представлены три разных способа построения сплайна Безье.

«Упрощенный» метод наименьших квадратов применяется для набора базисных функций, образующих матрицу А:

Рис.7. Пример нахождения кривой Безье для петлевого элемента. Слева-направо: «полный» метод наименьших квадратов, «упрощенный» метод наименьших квадратов, итерационный метод.

Ac

записанную Аналогично

для х-координат кривой, где записывается уравнение для

(5)

F(t) - искомая приближающая функция. нахождения коэффициентов при базовых

функциях для y-координат кривой. Исходя из условия минимизации невязки:

Лг = F(Xi ) " fi = £ AijCj " f = S 4^ " (Xi " (Xend - Xstart )ti - Xstart ) (6) jj

где fi - функция экспериментально полученных значений координат, получается матричное уравнение для нахождения искомых коэффициентов:

c = ((ataY At )f(7)

В нашем случае упрощение задачи заключается в необходимости нахождения обратной матрицы 2-го порядка, что может быть найдено непосредственно по формуле:

a reverse = 1 (+j) МЛ

(a b ^

что для матрицы A = I I, позволяет записать обратную матрицу в явном виде:

A 1

c d 1 (d -c a

(8)

det A ^- c a J

Как видно из рис. 7 (средний вариант) найденное таким образом представление сплайна является очень неточным. Поэтому следующим шагом необходимо уточнить найденное решение с помощью итерационного метода. Поскольку этот метод основывается на нахождении расстояния до кривой Безье, то требует решения алгебраического уравнения 5-го порядка. Действительно, в точке сплайна, находящейся на минимальном расстоянии от заданной точки: ds

dt

откуда получаем: s — = (X - X0)--+ (a - у0) = 0 .(9)

dtdtdt

Для нахождения решения применялся метод секущих:

tn+1 = tn -) , где f = (x - X0 )d- + (( - y0 )± .(10)

fn-1 - fndtdt

Найденное таким образом с помощью сплайнов Безье представление исходной траектории использовалось одновременно и для окончательного отбора кандидата на роль эталонной подписи и, фактически, для «тонкой» верификации подписи по ее форме.

Общая схема подпрограммы поиска эталонной подписи

С целью соблюдения оптимального баланса между производительностью подсистемы поиска и качеством ее работы был реализован иерархический, многоуровневый подход.

Первым шагом подпрограммы поиска являлся отбор возможных кандидатов для последующего анализа. При этом принимался во внимание следующий набор характеристик:

•Пропорции (ширина и высота) подписи;

•Координаты центра масс подписи;

•Количество сегментов;

•Количество петель;

•Максимальная длина штриха в вертикальном и горизонтальном направлениях;

•Количество вертикальных экстремумов;

•Отношение числа левоориентированных штрихов к правоориентированным.

На следующем шаге алгоритма найденные кандидаты передавались на вход процедуре поиска, описанной выше и работающей на основе скелетных представлений кривых. В текущей программной реализации алгоритм поиска отбирает три кандидата, доставляющих минимальные штрафы за несоответствие. На третьем шаге найденные три гипотезы проверяются на структурное соответствие с предъявленным образцом. И только