сдвинуты в сторону отрицательных величин. При этом степень сдвига выше выборок (табл. 2, рис. 3).

у дисперсных

Таблица 2.

Основные статистические характеристики отклонения средних значений численностей от генерального параметра рандомизированных (R) и дисперсных (A) выборок.

Примечание:

асимметрия, Ex - эксцесс, PL% - .вероятность соответствия нормальной функции.

As

DM5 Е

K-S d- 09760, p> 20; Lilhefcirs p-= 05

K-S d- 05551, p= .20, Lilliefors p=.05

DM10 R

<-S d=.DBB82, p> .20, Lilliefors p> 20

6 8 10 12

<-S d= 081 35, p= 05 ; Lilliefors p< 01

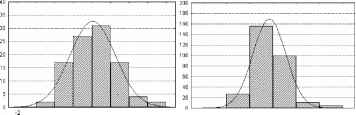
-1.5 -1 -0.5 0 0.5 1 1.5 2 K-S d- 07241, в= .20, Lilliefors p= .20

S-4-20246

K-S d= 03392, p> .20; Lilliefors p=- .20

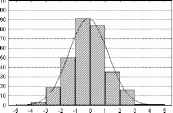
Рис. 3. Аппроксимация нормальной функцией эмпирических распределений ДМ рандомизированных (слева) и дисперсных (справа) размещений объектов в пространстве.

В отличие от выборочных средних, для которых генеральный параметр задавался в явном виде, независимо от конечного размещения организмов, величина их дисперсий априорно не известна, так как она зависит от многих параметров модели - количества точек инициации, скорости перемещения объектов, направления и времени его движения, а так же от размеров пробоотборника. Однако для изначально рандомизированных выборок (см. рис. 1, R) значение ожидаемой дисперсии известно - оно равно генеральной средней, так как ранее было показано, что в этом случае численности особей в пробах, как правило, распределены согласно Пуассоновчкой функции, так как спонтанное образование ложно агрегированных размещений особей событие довольно редкое. Действительно, усредненное среднее количество объектов в выборках для рандомизированных размещений приблизительно равно средней их дисперсий, однако диапазон варьирования дисперсий существенно выше, чем средних. Эта закономерность

еще сильнее выражена у выборок из дисперсных размещений объектов наглядно отражает величина их коэффициентов вариаций (табл. 3).

пространстве, что

Таблица 3.

Показатели вариабельности средних значений численностей и их дисперсий рандомизированных (R) и дисперсных (A) выборок.

коэффициенты вариаций средних и дисперсий.

дисперсий, Mcv, Dcv

Проверка на нормальность распределения дисперсий дала отрицательный результат во всех вариантах экспериментов. Тем не менее, оказалось, что оно с высокой степенью точности аппроксимируются логнормальной функцией, за исключением выборок, состоящих из 5 проб, отобранных из дисперсных размещений объектов (рис. 4).

Variable D5R ; diftributitti.: Ьодл*пш1 Kolinocjomv-Srnirnov d = 0734713, р = n.s Chi-Square: 13 39338, df= 7, p = 0631224

Variable D5A ; distribution: Lognormal

Kolmogorov-Srnirnovd= .1097337, p * .01 Chi-Square: 23.70391, df= 6, p= .0000694

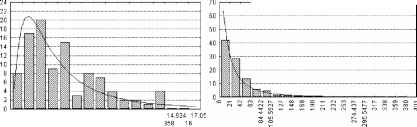
2.132

1.066

4.264 6.396 8.528 10.66 12.792 1 4.924 1 7.Of 5 33 7.462 Э.5Э4 1 1.726 13 Variable DIOR , iistriburion.: Logtionml Kolmogorrjv-Smirnrjv d = .0500271, p = n.s. Chi-Square: 2.305780, rjf= 4, p - .67971 90

Variable D10A ; dinnbutidtt.: LogjMimal Kolmogorov-Smirnovd = .0779821, p = .10 Chi-Square: 1 S.42069, df= 8, p = .01 S3077

Variable I25R , distribution: Lo^taimaJ.

Kolmogorov-Smirncw d = .0523856, p = n.s. Chi-Square: 1.7261 53, df= 3, p = 631 1395

Variable, distribution: Lo^tMmal

Kolmogomv-Smirnov d = .0635313, p < .20 Chi-Square: 6.03611 1, df= 5, p- .3027486

- 0 1 1 22 33 44 55 66 77

Рис. 4. Аппроксимация логнормальной функцией эмпирических распределений выборочных дисперсий рандомизированных (слева) и дисперсных (справа) размещений объектов в пространстве.

Рассмотрим распределение выборочных отношений дисперсий к среднему (K=D/M), которое часто используется в гидробиологических исследованиях в качестве простейшего

в

индекса агрегированности, а в модели сопряженных распределений Пуассона служит оценкой параметра q, определяющего соответствующую ему функцию из этого семейства (Хазов, 2004).

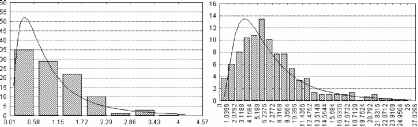
Эмпирические функции распределения этого показателя также хорошо аппроксимировались логнормальной функцией даже в области значений, соответствующих малым выборкам (рис. 5).

Variable К5Е ■ distribution.: Logiarmal Kolmogorov-Smirrov d = .0933755, p = ns Chi-Square: 9.783734, df= 2, p = .00751 30

Vunitк EJA , distribution.: Lo^iooml Kolmogomv-Smirnovd = .0730203, p < .10 Chi-Square: 25.75579, df= 1 4, p = .0278439

Variable K14R . distiitojlriori: Logtunmd

Kolmogomv-Smirnov d = .0351327, p = n.s. Chi-Square: 5.465209, df= 4, p= .2428308

Variable E10A ■ liistributltm1 Logpamial

Kolmogomv-Smirnovd = .0394393, p= n.s. Chi-Square. 2.109064, df= 5, p= .3330532

Variable K25R ; liistribuliciv Logpfomial Kolmogomv-Smirnov d = 0586942, p = n.s. Chi-Square: 4.690194, df= 3, p= .1959624

Variola КЭ5А • diaributi™ Logicimal

Kolmogomv-Smirnov d = 031 4203, p = n.s. Chi-Square, 7.176939, df= 8, p= .5176824

Рис. 5. Аппроксимация логнормальной функцией эмпирических распределений выборочных коэффициента K рандомизированных (слева) и дисперсных (справа) размещений объектов в пространстве.

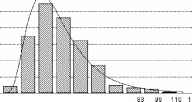
Данный результат представляется весьма важным, так как в этом случае логарифмы исходных значений эмпирических распределений хорошо аппроксимируются нормальной функцией, как показано для отношения дисперсии к среднему на рис. 6 для выборок объемом 10 проб из ложно контагиозных размещений объектов.

Variable LN10AK ; distribute.: Ifamal K-S d - .0394391, p - n.s. Lilliefors p = n.s. Chi-Square: 9.272843, df= 3, p= .3198429

0 0.2 0.4 0.60.8 1 1.2 1.41.6 1.6 2 2.2 2.4 2.6 2.S 3 3.2 3.4 3.6 3.8

Рис. 6. Аппроксимация нормальной функцией эмпирических распределений выборочных логарифмов коэффициента K дисперсных размещений объектов в пространстве.

Данное преобразование позволяет с большей точностью определять значение K. Действительно, после преобразования 6/=ln(K/) имеем среднее B=Lbi/n и его стандартное отклонение sB=(E(bi-b)2/(n-1))05, где n - объем выборки, тогда B находится в доверительном интервале Bmin=B-1.96sB, Bmax=B+1.96sB, проведя обратное преобразование получим