Kexpmin=exp(B\ Kec^=exp(Bmin) и Kexpmax=exp(Bmax). Вычисленные таким образом интервалы оценки параметра q СРП значительно точнее, определенных обычным способом (табл. 4).

Таблица 4.

Средние коэффициента K, их доверительные интервалы, вычисленные обычным способом и с использованием логнормального распределения.

Примечание: K, отклонение.

и его стандартное

Следует отметить, что оценка средних отношений дисперсии к среднему с использованием логнормального распределения дает более низкие величины, чем полученные обычным способом (см. табл. 4).

В заключение данного раздела рассмотрим еще один эффект влияния размеров выборки на ее вероятностно-статистические свойства, обнаружить который можно только на базе модельных экспериментов.

Как уже упоминалось выше эмпирические распределения численностей из псевдоагрегированных размещений объектов наилучшим образом описывались функциями семейства сопряженных распределений Пуассона: \P{ X1 = хь Х1 = 0,1...} = P( Х1) = p( xhAsl)

P{X2 = Х2, Х2 = 0,1...} = P(Х2) = 2Г =0P{X1 = X1}P{X2 = Х2 /X = Х1}

P{ X

0,1..} = P( Х; ) = X11=0

j-1

xj-1}P{ X

xj/ Xj-1 = xj-1}

P{X

xj / X

j-1

= Х

j-1} = p(xj; cxj-1) = exp( -cxj-1)сХ)-1/ xj!, где

относительный размер

пробоотборника, q = D( Xj )/ M (Xj ) = ^fi=1 c1 1 и j=frac(q)+1.

Для всех выборок, состоящих из 100 проб наилучшей аппроксимирующей были функции семейства СРП. Однако в серии экспериментов с 50 наблюдениями отмечено появление рядов с достоверным уровнем согласия с распределением Пуассона. Эта тенденция проявилась еще сильнее в сериях экспериментов с 25 пробами. Тем не менее, не смотря на высокую степень согласия с распределением Пуассона по критерию хи-квадрат (Qx>10%), вид эмпирических распределений не соответствует этой функции, в отличие от модели СРП (рис. 7).

ч астота

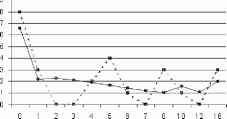
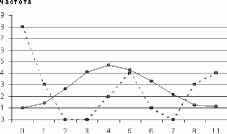
[" а Пуассон - -ш - выборка

Рис. 7. Графики эмпирического распределения (25 проб), СРП и Пуассона.

j

c

j

Обсуждение результатов.

Представленные результаты позволяют однозначно утверждать, что для широкого класса случайных размещений объектов в пространстве центральная предельная теорема для гидробиологических исследований справедлива для выборок, содержащих не менее 10 - 25 проб, в зависимости от степени дисперности пространственной структуры популяции. Однако в условиях реальной гидробиологической съемки необходимо ориентироваться на сильно дисперсные пространственные размещения особей. В обоснование этого утверждения приведем следующие аргументы.

Во первых, большинство организмов в природе демонстрируют сильно неоднородные размещения в пространстве (Downing, 1986).

Во-вторых, на основе рядов наблюдений небольшого объема невозможно провести анализ соответствия эмпирических распределений математической модели случайных размещений (СРП), что может привести к ошибкам интерпретации результатов, так как кроме них в природе существуют распределения организмов, детерминируемые внутрипопуляционными взаимодействиями между особями и/или действием факторов окружающей среды.

В третьих, разброс параметров в малочисленных выборках, даже из абсолютно рандомизированных размещений, слишком велик, что не позволяет провести однозначную идентификацию принадлежности каждой выборочной реализации к тому или иному расположению особей в пространстве.

Таким образом, если принять во внимание тот факт, что оценка средней численности по небольшим совокупностям проб обладает систематической погрешностью, то объем проб для корректного определения средней плотности популяции должен быть не менее 25 проб. Это то минимальное количество, которое необходимо отобрать на одном биотопе.

Выводы:

У объем выборки для полноценной статистической обработки, в том числе и для индикации типа размещений организмов в пространстве, должен быть не менее 25 проб;

^ распределение средних значений рядов наблюдений и их отклонений от генерального параметра соответствует функции нормального распределения;

> распределение дисперсий и их отношений к среднему распределено в соответствии с логнормальным законом;

^ оценка средней численности организмов на основе малочисленных выборок приводит к заниженным значениям этой характеристики.

Литература:

1.Айвазян С.А, Енюков И.С., Мешалкин Л.Д. Прикладная статистика. - М.: Финансы и статистика, 1983. - 471c

2.Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М: Наука, 1965. -

464 с.

3.Хазов А. Р Анализ гидробиологических данных и его программная реализация. -Петрозаводск: КарНЦ РАН. - 2000. - 155 с.

4.Хазов А.Р. "Исследование влияния размеров проб на вероятностно-статистические свойства выборок численностей организмов методом имитационного моделирования гидробиологической съемки" // Электронный журнал "Исследовано в России", 224, 2381-2390, 2004 г. http://zhurnalaperelarnru/articles/2004/224Pdf

5.Downing J.A. Spatial heterogeneity: evolved behavior or mathematical artefact. // Nature. -1986. vol. - 323. - № 6085. - P. 255-257

6.Lilliefors H. W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown // Journal of the American Statistical Association. - 1967. vol.64. - P. 399-402.