 |
 Как обустроить мансарду?  Как создать искусственный водоем?  Как наладить теплоизоляцию?  Как сделать стяжку пола?  Как выбрать теплый пол?  Зачем нужны фасадные системы?  Что может получиться из балкона? |
Главная страница » Энциклопедия строителя
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4]
страница - 0
К вопросу оценки точности приближенных вычислительных процедур метода анализа иерархий
Трофимец В. Я. (zemifort@inbox.ru ) Ярославский военный финансово-экономический институт
В работе [1] предложены четыре приближенные вычислительные процедуры нахождения главного собственного вектора матрицы парных сравнений, который после нормализации становится вектором приоритетов. Предложенные процедуры отличаются как точностью получаемых оценок, так и сложностью вычислительных действий.
Схема первой вычислительной процедуры состоит в следующем (1). Суммируются элементы каждой строки, после чего осуществляется процедура нормализации путем деления каждой суммы на сумму всех элементов матрицы. Первый элемент результирующего вектора будет приоритетом 1-го объекта, второй - 2-го объекта и т. д.
1 «12 ... a1n
a211 ... a2n
an1 an2 ... 1
A = Z a1 j
j=1
A2 = Z «2 j
j=1
An = Z anj
j=1
A1
w =--
1n n
ZZ aj
=1j=1
A2
w2 =-
2n n
ZZ aj
=1j=1
(1)
An
w=
nn n
nn
ZZ aj
=1j=1
Проанализировав процедуру (1), можно сделать вывод, что она эквивалентна процедуре нахождения средних арифметических по строкам матрицы с последующей их нормализацией.
Схема второй вычислительной процедуры состоит в следующем (2). Суммируются элементы каждого столбца, вычисляются обратные величины этих сумм, после чего осуществляется процедура нормализации путем деления каждой обратной величины на сумму всех обратных величин.
a 2
a
12
a
n2
a
1n
a
2n
A1 = Z a1 A2 = Z a 2 ... An =Z «п
i=1
i=1
i=1
A°6p = 1 A1
1
A2
1
An
A°6p
A°6p = Z А°6р
i =1
A°6p
1 a p A°6p
w2 =
А°6р
А°6р
wn = An
n a°6p
1
1
1
Проанализировав процедуру (2), можно сделать вывод, что она эквивалентна процедуре нахождения средних гармонических по строкам матрицы с последующей их нормализацией.
Схема третьей вычислительной процедуры состоит в следующем (3). Элементы каждого столбца делятся на сумму элементов этого столбца. Затем складываются элементы каждой строки новой матрицы, и эти суммы делятся на число элементов строки.
a" =
н a21_
a21 =
A
un1
A
a" = ^
A
A2
A2
2n : A2
a" =
nn
A
j=1
j=1
A" = Z a
n
j=1
W2 =
A1
n
AL
n
n
(3)
1
1
1
=1
=1
=1
Схема четвертой вычислительной процедуры состоит в следующем (4). Находится произведение элементов каждой строки, извлекается корень n-ой степени из полученных произведений, после чего осуществляется процедура нормализации путем деления каждого произведения на сумму всех произведений.
1^ a1n
a211 - a2n
an1 an2 ... 1
A1 = № a1 j
A2 =a2j
A
W2 =■
z A
=1
_Ai_
n
Z A,
(4)
A.
Z A
w1 =
=1
=1
Процедура (4) является процедурой нахождения средних геометрических по строкам матрицы с последующей их нормализацией.
В работе [1] указано, что процедура (4) обладает наибольшей точностью из рассмотренных, но теоретического или экспериментального обоснования точности процедур (1)-(4) не проведено. Ниже предложена схема и приведены результаты экспериментального обоснования точности приближенных процедур метода анализа иерархий.
Исследовались матрицы парных сравнений размерностью от 3 до 15 (в практике военно-экономического анализа матрицы размерностью больше 10-12, как правило, не встречаются). В основе проведенного вычислительного эксперимента лежал метод имитационного статистического моделирования (метод Монте-Карло).
Схема проведения эксперимента состояла в следующем (рис. 1).
Начало | ||
г | ||
Задание числа прогонов модели N1
Задание размерности прогона модели N2
Генерация случайной матрицы парных сравнений | |
г | |
Нахождение я0 max | |
г | |
Расче | т ОО |
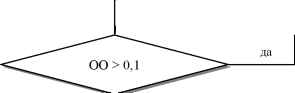
нет | |
г | |
Нахождение | |
max max | , я3 , я4 max max |
1 | г |
Рис.1. Схема проведения вычислительного эксперимента по обоснованию приближенных вычислительных процедур метода анализа иерархий
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4]