Исследование напряженного состояния в шестиугольной пластинке, ослабленной двумя круглыми отверстиями с

шероховатостью

Калбиев.Р.К (elektroset@box.az)

Азербайджанский Архитектурно-строительный университет г. Баку, Азербайджанский Республика

Развитие современной техники невозможно без наличия надежных, научно обоснованных и экспериментально подтвержденных методов расчета напряженного состояния деталей машин и элементов конструкций.

Работоспособность деталей машин и элементов конструкций в виде пластин зависит от наличия в них концентратов напряжений типа полостей, щелей, шероховатостей и т.д. Поэтому изучение распределения напряжений и деформаций около таких дефектов представляет теоретический и практический интерес.

Одна из важнейших проблем механики деформируемых твердых тел - анализ их напряженно-деформированного состояния около указанных дефектов.

В работе на основе методов теории функции комплексного переменного и конформного отображения рассмотрены напряженное состояние для неодносвязных областей. Искомые функции ищутся в виде степенных рядов, коэффициенты которых определяются решением совокупности некоторых бесконечных систем линейных алгебраических уравнений.

Работа посвящена вопросу напряженного состояния шестиугольной пластинки, ограниченной снаружи шестиугольным контуром а изнутри симметрично расположенными двумя близкими круговыми отверстиями. Считается, что реальная поверхность детали имеет микро или макроскопические неровности технологического характера, образующие шероховатость.

Исследуем однородную изотропную пластинку, состоящую из трехсвязной области S ограниченной снаружи шестиугольным контуром L0, а изнутри симметрично расположенными двумя близкими круговыми отверстиями L1 и L2 с одинаковыми радиусами r1 ( r1 = r2 ).

Введем полярную систему координат. Представим границу внутренних контуров L1 и L2 пластинки в следующем виде

p(e)=ru+5u(e)

Запишем второе слагаемое в правой части уравнения в следующем виде

5u(e)=sHu(e)

здесь s-малый параметр, равный отношению высоты наибольшего выступа профиля к радиусы отверстия или отношению глубины наибольшей выпадины профиля к радиусу отверстия; Н1;2(е)-функция, независящая от малого параметра. Компоненты тензора напряжений ищем в виде [1] разложений по малому параметру s:

0r = Of) + £0f) + ...

ае = о(е0) + еа™ +...( 1 )

те = те0) + 41) +...

в которых для упрощения задачи пренебрегаем членами, содержащими малый параметр s в степени выше первой. В соотношениях (1) or(0), ое(0) и Tre(0) - напряжения нулевого приближения, а or(1), oe(1) и Tre(1) -напряжения первого приближения. Каждое из приближений удовлетворяет системе дифференциальных уравнений теории упругости.

При этом на контуры пластинки действуют кусочно-равномерно распределенные нагрузки с интенсивностью Р0, Р1 и Р2 соответственно под углом 2а0; 2а1 и 2а2 (Рис. 1).

Как известно [1], определение напряженного состояния в данной области приводиться к нахождению двух аналитических функций pp(z) и \/(z) комплексных переменных, удовлетворяющих определенным граничным условиям:

<p(t) + <p(t) + фТД) = fj(t) + Cj, t e Lj , (j = 02)

Здесь t - аффикс точек контура Lj; Q -вещественные постоянные (одну из которых, например С0, примем равной нулю, а С1, С2 определяются по ходу решения задачи). fj(t) примем в виде

степенного ряда, т.е.

f j (t) = £ HVj)Tv (j = 0, 2 )

V=-oo

т-аффикс точки контура единичной окружности, HVj) определяются из условия непрерывности функций fj(t) на контуре Lj. Аналитические функции pp(z) и \/(z) в трехсвязной области S ищем в виде

<p(z) = I a(f)k + z b<1)(-L)k + 1 e<1)(^)k k=о A k=1 k z-e1 k=1 k z + e2

k=0 k A k=1 k z - e1 k=1 k z + e2 На основе геометрических и силовых симметрии коэффициенты a^b^e^, A^B^eI^ ( = 0,N) будут вещественными.

Ф У

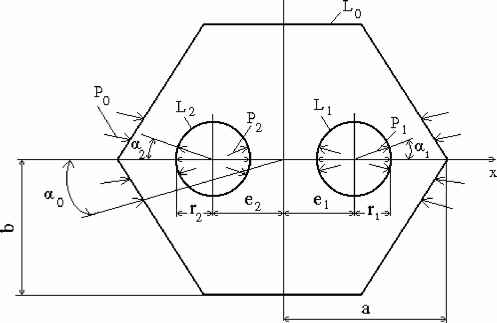
Рис. 1.

Так как контур L0 отличен использовать функции [3]

z = АтГ 1 + — 1(2)

тч J

от окружности, при решении поставленной задачи будем

a + b I i a - b

где A = ——; m =--

2 1 1 a + b

а и b соответственно радиусы окружностей, описанных вокруг шестиугольник и вписанных в шестиугольник L0; q-число осей симметрии (число сторон), q=6.

Знак m определяет форму расположения контура L0 в плоскости z=x+iy. Когда m>0, большая ось симметрии кривой совпадает с осью абсцисс, а когда m<0, то малая ось симметрии кривой совпадает с осью абсцисс. Очевидно, что в (2) при m=0 контур L0 превращается в окружность, а при q=2 в эллипс. При q>2 абсолютное значение m может быть определено по формуле:

II161

m =-— и для шестиугольника q=6; m = —

(q -1)225

После некоторых выкладок и преобразований [1] находят коэффициенты

aj^.b^.e^, a[,1),b[,1),e[,1) (k = 0,N). После этого по формуле Колосова-Мусхелешвили

определяется компоненты напряжений or, ое в точках произвольно взятых центральных сечений пластинки.

Перейдем к решению задачи в первом приближении [2]. Граничные условия этой задачи имеют вид

9l(t)+^1(t) + = f(1)(t) + C(1), t e L; , (j = 0T)

e_

f(1)(t) = —irj j (Xn + iYn)de (j = 0,2)

0

Xn + iYn = —(N + iT)eie

При r=r1=r2

N

ч r=r1

-H(e)

(0)

re R de

Т

r(1)l 1 1 er k=ri

— I

(0))i dH(e)

R de

—H(e)-

dr<°>

er

dr

f(1)(t) = 2 Htj,1) tV ; т = eie

Дальнейший ход решения задачи аналогичен нулевому приближению [2]. Для удобства в первом приближении сохранены обозначения для искомых коэффициентов. Таким образом в

первом приближении для определения коэффициентов akl),bkl),ekl),Ak1),Bk1),Ek1) (k = 0,N)

получены 6 группы бесконечных систем линейно алгебраических уравнений, отличающихся от нулевого (что очень удобно при расчетах на ЭВМ) правой частью системы.

Полученные решение в зависимости от параметров шероховатости, геометрических и силовых факторов можно распространит на решение многочисленных частных задач.