Расчет туннельного коэффициента для электрона в случае потенциала, заданного во внутриатомном масштабе для тонкослойного материала: часть первая

Зайцев Н.А., Матюшкин И.В. (matyushkin@mikron.ru)

ОАО «НИИ молекулярной электроники и Микрон»

Тема данной работы инициирована проблемой математического моделирования токов утечки, имеющих в основном туннельную природу, через ультратонкий (1-5нм толщиной) подзатворный диэлектрик, например, диоксид кремния при работе субмикронного МОП-транзистора. Имеющиеся экспериментальные данные указывают на существование немонотонности вольтамперной характеристики Ig(Vg) для тока утечки Ig [1,2,3], особенно в области малых напряжений Vg<~0.5B [4,5]. Кроме того, модельные расчеты дают заниженную оценку для такого туннельного тока, чем это наблюдается [6,7]. При Vg=1B и толщине подзатворного SiO2 ^ж=1нм плотность тока утечки ~10A/см . Таким образом, при переходе полупроводниковых приборов в наномасштабную область актуальна задача усовершенствования существующих моделей туннелирования.

Предлагаемый нами подход основан на учете внутриатомной структуры потенциала, создаваемого атомами на дистанции туннелирования, который воздействует на волновую функцию электрона, попавшего в зону проводимости полупроводникового материала. Он не предполагает использования приближения эффективной массы и при самых общих условиях годится не только для SiO2 или альтернативного подзатворного диэлектрика, но для произвольного материала, через ультратонкий слой которого (5-20 моноатомных слоев) происходит туннелирование. Вместе с тем развиваемая в статье модель, представляющая простейшую реализацию данного подхода, обладает весьма узкими рамками применимости, а расчетные кривые в большинстве своем допускают только качественную интерпретацию. Тем не менее, с помощью модели удается объяснить экспериментально наблюдаемую немонотонность Ig(Vg), основываясь на явлении резонансного туннелирования.

Во избежание недоразумений заметим, что здесь и далее под «туннелированием» имеется ввиду прямое и неупругое, т.е. без рассеяния на фононах, туннелирование электрона, находящегося в зоне проводимости одного материала в

область проводимости другого материала. Первая часть работы преимущественно только суммирует известные факты. В п.1. мы коротко рассмотрим связь между задачей моделирования тока утечки и поиском коэффициента проницаемости потенциального барьера. В п.2. проведен анализ основных уравнений и ограничивающих предположений стандартной модели туннелирования. Расчетные зависимости в п.3. отвечают на вопрос, в какой мере применима стандартная модель для узких (по ширине) и мелких (по энергии) барьеров. В п.4. мы рассмотрим адекватность подстановки кулоновского потенциала как возможной формы барьера и наметим возможные пути решения этой проблемы через использование модели Томаса-Ферми. Во второй части данной работы будет предложена адаптация трехмерного уравнения Томаса-Ферми для одномерной задачи, получен вид внутриатомного потенциала, исходя из одномерного уравнения Томаса-Ферми, а также проанализированы результаты расчетов туннельного коэффициента многобарьерной системы.

1. Связь туннельного тока и туннельного коэффициента Для расчета плотности туннельного тока j [А/м ] через ультратонкий диэлектрик в МОП-структуре можно использовать следующую формулу [5,8]:

Здесь :e- элементарный заряд, kbT- температурный больцмановский множитель, m c-

эффективная масса электрона в направлении туннелирования в зоне проводимости диэлектрика, Efm и Efs- уровни Ферми в металле и кремнии соответственно, Ec-

граница зоны проводимости диэлектрика на границе кремний-диэлектрик, E- энергия электрона, Ex- его энергия в направлении туннелирования.

Не только туннельный ток, вычисляемый согласно (1), зависит от концентрации электронов по обе стороны от барьера, но и сам туннельный коэффициент T(Ex), как мы увидим позднее, зависит от налагаемых на волновую функцию условий слева и справа. Кроме того, если учитывать динамику, то, например, квантование носителей в инверсионном слое будет изменяться по мере проникновения электронов из приповерхностного слоя кремния в металл. Математически это описывается самосогласованной системой уравнений Шредингера-Пуассона [9,10,11]. Присутствие логарифма от функции Ферми-Дирака в

(1)

подынтегральном выражении (1) связано с подстановкой выражения для двумерной плотности электронов, находящихся слева и справа от барьера (туннелирование может происходить и в обратном направлении). Далее, предполагается сохранение для туннелирующего электрона компоненты импульса, параллельной границе раздела полупроводник-диэлектрик. Заметим, что интегрирование по dEx приводит к появлению функций Эйри в подынтегральном выражении. При ненулевом напряжении на затворе и в предположении трапециидальности (рис.1) барьера можно получить формулу Фаулера-Нордгейма:

Здесь А,В- константы, F~Vg/td - напряженность поля внутри диэлектрика толщины td, и~ЕС(Г-Ес (Ecd- уровень дна зоны проводимости диэлектрика) - высота барьера, во многом сходная с работой выхода (исторически изучение туннелирования в 20-х гг. началось с опытов по автоэлектронной эмиссии с поверхности металла в вакуум, откуда эта формула перекочевала в микроэлектронику).

Таким образом, правильность модельных предположений относительно туннельного коэффициента T(E) может быть проверена только косвенным образом по вольтамперной характеристике, построенной в координатах lg(Ig/Vg2) vs (-1/Vg).

Отметим также, что экспериментальному измерению подлежит ток, лишь

усредненный по площади затвора, и шероховатость подзатворного диэлектрика [12] усложняет наблюдение предсказанных теоретически кривых.

AF

BU

3/2

U

eXp("

F

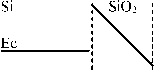
металл

Рис.1. Идеализированная МДП-структура в стандартной модели при приложенном напряжении на затвор. Один из основных путей туннелирования: из зоны

Ev

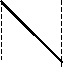
2. Анализ стандартной модели для проницаемости барьера Сама проницаемость барьера определяется (3) через отношение падающего и прошедшего через барьер (рис.2) потоков частиц, причем существенную роль здесь