О превращении фононного конденсата при фотодиссоциации поляронов Ландау-Пекара

Мясников Э. Н. (1), Мясникова А. Э. (2), Мастропас З. П. (mastrozin@mail.ru) (1)

(1) Ростовский государственный педагогический институт (2) Ростовский государственный университет

В настоящей статье методами теории квантово-когерентных состояний выводится аналитическое выражение для расчёта спектров фотодиссоциации поляронов Ландау-Пекара [1] сильной связи при квантовом рассмотрении поля поляризации. В

классическом пределе полученное нами выражение совпадает с известным результатом

Эмина [2]. Квантовый результат отличается от классического вследствие того, что при квантовом рассмотрении поля поляризации в одном акте фотодиссоциации полярона Ландау-Пекара может излучаться как большое число фононов, так и малое (вплоть до одного), и лишь в среднем энергия излучаемых фононов совпадает с энергией поля поляризации в поляроне (равной 2E p).

Так называемый поляронный гамильтониан имеет вид:

где Ь, и Ь, - операторы рождения и уничтожения фонона k -ой гармоники фононного

состояния с деформацией фононного вакуума, удобно произвести преобразование

гамильтониана и волновых функций с помощью унитарного оператора сдвига

Этим преобразованием полевые операторы Ь, и Ь~ превращаются в новые операторы поля Ь+ и Vt по схеме: Ь = UtЬЛ]- = Ь — dk, Ь+ = U,Ь,U-1 = Ь,+ - d* . В

кккк к ккккк к ккк

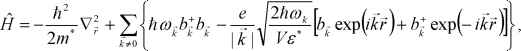
(1)

поля, V - объем кристалла, S

SQSmj(s0 — sj). Для того, чтобы исследовать

качестве параметров d~ унитарного преобразования естественно выбрать такие, чтобы

значения поляризации

(3)

к *0

равнялись квантовым средним значениям поляризации во всех точках кристалла в поляронном состоянии (деформации фононного вакуума электрическим полем носителя

заряда ). В этом состоянии системыиотличны от нуля и равны

соответственно dк и d *, а (b^j = (b+Sj = 0.

Фактически, в теории поляронов Ландау-Пекара вектор основного состояния системы выбирают в виде

\d) = щ (d- R)exp\I (d,b++ - dfo Л

(4)

где 0^ - вектор основного состояния фононной подсистемы в отсутствии деформации

вакуума, R - произвольный вектор прямого пространства, а Ц/0 (r) - нормированная

волновая функция электрона в основном состоянии полярона. Для такого состояния системы (4) среднее значение гамильтониана (1) можно представить в форме:

(d# d)

h2

-v2 +

+

к*0

h(DT

к

2m*

d: d k + (d\b + b r\ d)

к к \ i к к i /

2^PL (dkexp(ikr Кdkexp(- ikr)]

(5)

В этом выражении ^db+bd) представляет собой среднее число fl~ фононов к-ой моды, которое в основном состоянии системы должно равняться нулю. Вводя обозначения d~ = \d~ exp(/^), приведем функцию (5) к виду, удобному для

нахождения ее минимума по переменной

d ,

Условие минимума по

d ,

приводит в

рассматриваемом случае центральной симметрии состояния (4) к соотношениям

(dtfd} — (— VА = —£2ne2(vS,2)Xr,\{p)=-YjicOkd,d, ,(6)

где Г, (3) - k -я Фурье-компонента функции ^0(г) с некоторым варьируемым параметром /. В системах с сильным электрон-фононным взаимодействием хорошие результаты дает использование предложенной Пекаром [1] волновой функции носителя

(//„(r,3)=(7л/?_3)/2(1 + //r)expV /r). Минимизация (6) по переменной / приводит к Пекаровским значениям для / и энергии связи полярона E p , энергия

деформации фононного вакуума flCO^, d, = 2Ep.

Фотодиссоциация поляронов происходит в результате взаимодействия электромагнитной волны с частотой Q с носителем заряда в поляроне. Оператор

указанного взаимодействия имеет вид п int =

Hint = eh2(т*с) 1 (£i)exp[zV — ,))], где h, -

импульс носителя, Q - волновой вектор электромагнитной волны, A - амплитуда её

вектор-потенциала, связанная с интенсивностью волны I = 01А2/2жНс. По золотому правилу Ферми вероятность перехода квантовой системы в единицу времени из состояния ^ в состояние f^ под действием оператора Hint есть

W =—

f\Hint d{Et — Ef ). Начальное состояние - основное состояние полярона

^ = -\J 1п/3 3 (1 + /3Г)exp(— //Гd^j в поле электромагнитной волны,

<?

Ez = — Ep + HQ. Конечное состояние системы f) = L ^ exp ((Г}),

<?

т* + h(DV , где V - сумма чисел V- из набора fy- }. Тогда