u (x, y, t) = xX (y, t), v( x, y, t) = - J W (s, t )d< - ЯЛ-1у [X (y, t) - X yV (t)] - X x 2F (t) (3.1)

0

Перемещениям (3.1) соответствуют деформации

ex = X(y, t), ey = -W(y, t) - ЯЛ-1 X(y, t),= exz = eyz = = 0(3.2)

Здесь, как и ранее, X(y,t)=U(t)+yV(t).

Пусть область упругости -h < y < y*(t), где y*(t) - неизвестная заранее граница. Тогда напряжения, соответствующие перемещениям (3.1) и деформациям (3.2), имеют вид = 4/(Я + и)Л-1 X (y, t) - ЯW (y, t), Oyy = -ЛW (y, t)

Ozz = -XW (y, t) + 2Я/Л-1 X (y, t),=OXZ = Oyz = 0

Из уравнения равновесия dOyy (y, t)/dy = 0 следует dW (y, t)/dy = 0. С учетом условия (1.9)

отсутствия напряжений на нижней границе плиты получаем W(y,t)=0 при -h < y < y*(t). Таким образом, в области упругости

Ox = 4/(Я + и)Л-1 X (y, t), OzZ = 2Я/Л-1 X (y, t)

Oyy =Oxy =Oxz =OyZ = 0, -h<y <y.(t), t > 0.

Поврежденный материал плиты занимает область y* < y < h. Будем считать, что в этой области перемещения и деформации также выражаются формулами (3.1), (3.2), в которых функция W(y, t) не равна тождественно нулю. Инварианты I1, J и девиатор тензора деформаций вычисляются по формулам

I = 2M-1X(y, t) - W(y, t), J2 = l2X2(y, t) + 2KV-1W(y, t)X(y, t) + %W2(y, t) (3.4)

3Л*хх = (3Я + 4/) X (y, t) + ЛW (y, t), 3Л£уу = -3KX (y, t) - 2ЛW (y, t)

3Л^ =-2/X (y, t) + ЛW (y, t) Из формул (3.4), (3.5) и кинетического уравнения (1.3) следует, что поврежденность ср = <p(y, t). Напряжения в повреждающемся материале задаются выражениями

Ox =(4/(Я + и) - (Я + X и)£)Л-1 X-(Я + Y3^)W - a<p

Oy = KЛ-l^X-(Л-2/3{)W - app, =(2//-фху = 0, t = a<p/J На границе y = y*(t) , разделяющей области упругого и поврежденного материала, выполняются условия сопряжения: равен нулю параметр поврежденности и непрерывны перемещение и вектор напряжений. С учетом формул (3.1), (3.3), (3.6) условия сопряжения сводятся к двум соотношениям

X (y*(t), t) = Лg /(2/ap +1Ла8), W (y.(t), t) = 0(3.7)

Пусть напряжение Oyy =0 при всех y*(t) < y < h . Тогда функция W(y,t) определяется равенством, которое следует из второй формулы (3.6)

(M - 2/3 a<p)W = (asK Л-1 X - apJ )р(3.8)

где р(у, t) удовлетворяет дифференциальному уравнению (1.3), а инвариант J(y,t) задан

выражением (3.4). При таком задании функции W(y,t) граничное условие Oyy(h,t)= 0 и

условия сопряжения (3.8) выполняются тождественно.

Входящие в выражения (3.1) - (3.8) функции U(t) и V(t) связаны с растягивающей силой и изгибающим моментом соотношениями

(3.5)

(3.6)

N(t) = 8/hЯЯ+UUU(t)- Г

ЛyJ(t

Mz (t) = 8/h3(t)-J

Я + -^W (y, t) + a<p + ЯЯ+ЛЛии- t;X (y, t)

k " Я + 3^ W(y, t) + app(y, t) + Я+ЛЛЕ%X(y, t)

dy

ydy

Таким образом, при заданных функциях U(t) и V(t) решение об изгибе и растяжении сводится к совместному решению кинетического уравнения (1.3) с начальными данными (1.10) и конечного нелинейного соотношения (3.8).

Нелинейная краевая задача (1.3), (1.10), (3.8) исследовалась численным образом в безразмерных переменных

t = t/т, y = y / h, x = x/h, a =ац/a0, ф = ф/ e0, UU = u /(he0), v = v/(he0),

U = U / e0, V = hV / e0, W = W / e0

0

1,

Л = Л / и,

a

где h

полутолщина плиты, e0 =Лg /(2/jap +1 Лas) - характерная деформация, a0 = jue0 -

характерное напряжение, время релаксации т - характерное время. При таком выборе безразмерных величин все они - величины порядка единицы. Для краткости далее черта над безразмерными переменными опущена. Тогда кинетическое уравнение (1.3) и начальное условие (1.10) может быть записано в виде

ф + фп = H(f) f (X,W), c(y,0) = 0, -1 < y < 1, t > 0(3.9)

f (X, W ) = apb-1 (2мЛ-1 (X -1) - W ) + asbl ( J (X, W) -1)

J (X, W ) = Jl2 X2 + 2K Л-1 WX + 2/ъ W2 где H (f) - функция Хевисайда. Функция X (y, t) = U (t) + yV (t) - заданная «нагрузка».

Уравнение (3.8) при переходе к безразмерным переменным не меняет своей формы. При решении нелинейного уравнения (3.8), которое сводится к алгебраическому уравнению четвертого порядка, возникает проблема отбора вещественных корней. Поэтому удобно использовать вместо (3.8) дифференциальное уравнение с начальным значением W(y,0) = 0 . Дифференцирование по времени (3.8) приводит к уравнению

(Л/ - Xa<< + J \уъW + KЛ-1 X+ apc))w =

= ((a<KЛ-1)X + уъasW - apJ)ф + (asKЛ-1ф - J"1 (l2X + KЛ-^+ ap<)

Таким образом, задача сводится к задаче Коши для системы двух обыкновенных дифференциальных уравнений (3.9) и (3.10).

При численном интегрировании принимались следующие значения параметров материала: и = 1, Л = 2, ap = 1, Ь = 1, 1 < a< < 2 . Показатель кинетического уравнения n =1

или n =2. Траектория нагружения задавалась выражением V(t) = rt, t < t0, V(t) = rt0, t > t0,

U(t) = kV(t), где t0

(3.10)

время нарастания нагрузки,

скорость нагружения,

к

коэффициент пропорциональности между изгибом и растяжением.

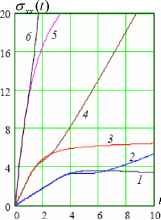
На рис.3 приведена зависимость для поверхностного слоя y=h плиты при чистом изгибе (U(t)=0) с постоянной скоростью (r=0.3, 1.0, 5.0). Кривые 1,3,5 соответствуютлинейной

кинетике (n=1), кривые 2,4,6 соответствуют n=2. Рис^ соответствует a< = 1.1 , рис.3Ь -

a< = 1.5. Можно видеть, что

решение сильно зависит от показателя n и коэффициентов ap, as, Ь . При малых значениях

a< , когда положителен длительный модуль сдвига

а)

Ъ)

Рис.3.

2/4 = 2// - a2 / b > 0, рост деформаций приводит к монотонному увеличению напряжений,

причем для n=2 этот рост сильнее, чем при n=1. Отмеченная особенность справедлива для любых скоростей деформирования. В случае если длительный модуль отрицателен, равномерное деформирование материала с показателем n=1 приводит при всех скоростях деформации к падающей зависимости a3D. (exx). Более интенсивное падение напряжений

происходит в материале с меньшим показателем кинетики. Причем максимум напряжения при малой скорости достигается в более поздний момент времени (но при меньших значениях деформации) по сравнению с высокоскоростным деформированием. При n=2 зависимость о^. (exx) остается в целом растущей, но для нее при деформации к 2e0

появляется область смены знака кривизны, которая с уменьшением скорости деформации превращается в «зуб текучести» [6,14]. Особенно ярко этот эффект проявляется при малой скорости деформирования.

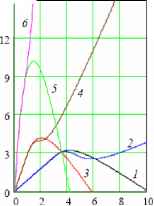
На рис.4 представлена зависимость a3D.(у, tt) для последовательности моментов

времени t,. Кривые 1-4 соответствуют t=2, 4, 6, 7.5, 10. На рис. 4а представлены данные

для линейной кинетики п=1,

2.83

1.67

0.5

-0.67

-1.83

2.33

1.67

0.5

-0.67

-1.83

-1 -0.6 -0.2 0.2 0.6 Г

y

-1 -0.6 -0.2 0.2 0.6

7

Рис.4.

уменьшение растягивающих напряжений по сравнению

на рис.4Ь -для n=2. Скорость деформированияr=0.2.

Параметрыматериала

/ = 1, Л = 2,

ap = 1, as = 1.5, b = 1.0.

Коэффициент к = 0.5 . Видно, что наличие растяжения приводитксдвигу

нейтральной линии изгиба в областьотрицательных

значений у. Эволюция поврежденности вызывает с напряжениями в состоянии упругости. В отличие от решения задачи об изгибе плиты из идеального или упрочняющегося упругопластического материала полученное распределение носит немонотонный характер. Для материала с модулем < 0 и параметром n=1 распределение имеет максимум вблизи границы между упругим и поврежденным материалом. При кинетическом параметре n=2 зависимость азх (у, tt) более сложная. Она

характеризуется локальным максимумом и локальным минимумом, координата которого с ростом времени стремиться к координате локального максимума, что приводит к образованию между ними зоны больших градиентов напряжения о^., соответствующей

«зубу текучести» на диаграмме «напряжение - деформация».

4. Макроразрушение плиты при изгибе и растяжении. С ростом деформаций материала может возникать реологическая неустойчивость., которая сопровождается образованием поверхностей локализации деформаций, являющихся прообразами макроскопических трещин. Найдем условия возникновения и формы этой неустойчивости в рассматриваемой задаче. Будем следовать работам [10,11], в которых реологическая неустойчивость связывается с нарушением условия Адамара [8,9].

В [3,11] показано, что скорости нестационарных характеристик (с ф 0 ) системы динамических уравнений для рассматриваемого материала определяются формулами

рс^е,?,n) = M + P±(P2 -Q) 2 P(e,p, n) = L + £n • N 2(e) • n

£ = asq>/J, M = /-£/2,

Q(e,<p, n) = £L (n • N 2(e) • n - (n • N(e) • n)2)

L = Я + ju-g/6

(4.1)