кристаллической структуры, применение зонного подхода не совсем корректно. Если для макроскопических слоев успехи такого подхода, выводящего за рамки модели внутриатомный потенциал, неоспоримы, то для нанослоев попытки «спасти» эффективную массу (например, введением пространственно-распределенной m (x,y,z) [16]) лишь затеняют существо проблемы.

2.Трапециидальность (или треугольная форма) барьера. Делаются попытки учесть влияние на его форму сил зеркального отображения электростатической природы, возникающие со стороны металлического электрода [5]. В работе [11] авторы попытались учесть внутриатомный потенциал, однако, весьма абстрактным путем.

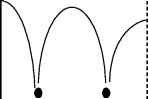
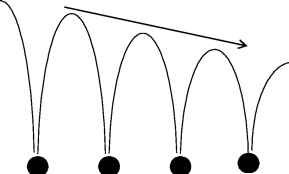
3.Единственность барьера. При рассмотрении подзатворного диэлектрика, толщина которого составляет единицы (до 20) моноатомных слоев, на атомарном уровне выясняется существование в действительности многобарьерной системы (рис.3)

4.Предположение плоских волн («полочек» потенциала) в качестве граничных условий. К сожалению, данное ограничение трудно обойти. Вместе с тем именно в этом вопросе, вероятно, имеется важная связь туннельной задачи с задачей квантования носителей в приповерхностном слое полупроводника.

-^

0

поверхностный, частично разупорядо-ченный слой кремния

<уровень вакуума> диэлектрик (SiO2)

металл или

Si*

Рис.3. Потенциальная диаграмма реальной МОП-структуры при приложенном к затвору напряжении. Условные (для одномерного случая!) границы раздела кремний-диоксид кремния, диоксид кремния-металл показаны штриховой линией. Наклонной стрелкой отображается общее влияние напряжения на затворе на форму потенциала. Небольшими кругами обозначены атомы (атомные кластеры), создающие сингулярности для U(x)<0, за ноль принят уровень вакуума. U(x)-потенциальная энергия одного электрона, попавшего в зону проводимости, связанная с электростатическим полем ядер и остальных электронов.

a0 = 10-10 м, U0 = 1.6* 10 19 эВ, k0 =

mU 0 a0

x = £ As + A + A^X)aQ, ¥(x) = W(X), W(1 + 0) = W(1 - 0),+ 0) = ^¥(1 - 0),

12m

initial :¥^W (1,0) -> (1,0), (0,-^) -> (0,-КД k1 = J— U0(E - U1).(9)

final: W^y/ (Re WJmW) -> (Re у,Ьп у), (ReЧ",ГшW) -> ReW,ReW), kn =^ ^ U 0( E - Un).

Весь потенциальный профиль разбивался на n участков, соответствующие барьеру, яме или барьеру-яме (для одного атомного остова), причем для каждого из них размерной ширине ai (i=1,n) соответствовало изменение безразмерной координаты Хе[-1,1]. Сужая задачу, можно интерпретировать U(X=0) как потенциал в центре атома. Первый и последний участки принимались за «полочки», т.е. U1(X)=const1, Un(X)=const2. Как обычно, волна падает справа налево, переводя начальные условия в конечные (10):

Несмотря на отмеченные недостатки, стандартная модель достаточно проста и нетребовательна в отношении вычислительных ресурсов. Поэтому, улучшая ее, желательно добиться компромисса между сложностью уравнений модели и временной стоимости расчета.

3. Расчет туннельного коэффициента многобарьерной системы путем

решения 1D уравнения Шредингера

Коэффициент T(E) (индекс для простоты писать далее не будем) для электрона, туннелирующего через многобарьерную систему, аналогичную изображенной на рис.3., можно найти аналитически, если известно решение одномерного уравнения Шредингера (это следует из определений [3]). Данная модель реализована нами в виде компьютерной программы, результаты расчета, полученные с ее помощью, представлены на рис.4-7. При составлении математических моделей общемировая практика показывает удобство использования метода обезразмеривания; далее заглавными буквами будут обозначаться безразмерные величины, а маленькими-соответствующие им размерные (в системе СИ):

- k2( x yv

d

dx

x_ x

{ dX

Легко получить, исходя из (3), выражения для туннельных коэффициентов (11):

D \ 2 , /D C \2

final

(A + — у + (B - —у к/ккк

n

Данное выражение может быть переписано в виде (12):

T -4к^--- , R _ 1 + 2 4 • Ь*?У/к;)- (12)

И + \И/ К1 - 2 ^/ К )„r,,„lИ + \И / К\ - 2 МИИ / К )„„„„,

Сумма T+R=1 из физических соображений. Математически покажем этот неочевидный факт для (11) (ведь на значения A,B,C,D, казалось бы, не наложено ограничений). В отсутствии магнитного поля уравнение Шредингера распадается на два независимых для мнимой и действительной части и может быть рассмотрена как система линейных дифференциальных уравнений с переменными коэффициентами. Для этой системы значение определителя Вронского сохраняется (см.(12)) и для решений задачи Коши для условий (1,0) и (0,-1) равно (-1). При этом мы ссылаемся на теорему Остроградского-Лиувилля.

Система (9-10) решалась численным методом Рунге-Кутты (по схеме 1:4:4:1). Вначале приведем результаты для тестового барьера на рис.2. Целесообразно проверить, экстраполируя результаты для Т(Е), полученные для тестового случая, какую погрешность дает формула Гамова для мелких (по энергии) и узких (по ширине) барьеров или ям атомных масштабов. Такую оценку, разумеется, сравнительно легко получить, исходя из показателя экспоненты, но надежнее и нагляднее решить эту задачу численно. Результаты численного расчета весьма хорошо совпадают с теоретическим предсказанием, что свидетельствует о действенности выбранного численного метода. Они также указывают: а) на сильную степень влияния значения эффективной массы на расчетное T(E),- например, вблизи потолка барьера для m =1 (в массах свободного электрона) T(0)=0.33, а для m =0.16 T(0)=0.76; б) в случае надбарьерного отражения (E>0) T(E) приближается к единице

*

лишь при энергии порядка нескольких высот барьера E~5Ub; в) при m =1 (в отличии

*

от m =0.16) наблюдается слабая одиночная осцилляция T(E) в области надбарьерных

dV _

_V(Rei/Л ( ИЛ(1 0 1 (AC Л ( Л„Л\

(10)